Il racconto contenuto in questo editoriale, molto particolare, inizia in un giorno dell’inverno del 1961, in un laboratorio del Massachusetts Institute of  Technology (il celebre MIT) e il protagonista della prima parte del racconto è il dott. Edward Lorentz, meteorologo americano, considerato il padre della meteorologia moderna, oltre che uno dei principali scopritori della teoria del caos.

Nel periodo considerato, Lorentz aveva iniziato a gettare la basi della moderna previsione meteorologica, inserendo, in uno dei primi modelli di supercomputer, dati riguardanti valori di temperatura, pressione, umidità dell’aria ecc. e valutando, in funzione dello scorrere del tempo, come tali valori si modificassero in una determinata area. Un primo abbozzo di previsione al calcolatore insomma, oggi comunemente usata in tutte le elaborazioni che i meteoappassionati consultano quotidianamente.

In queste elaborazioni, nell’inserire i valori provenienti dalle misurazioni effettuate nei vari luoghi del mondo (più probabilmente riguardanti un’area circoscritta come quella degli Stati Uniti, ancora la potenza dei computer era limitata), Lorentz, come tutti gli scienziati del periodo, non considerava un problema l’eventuale approssimazione dei dati di input; ad esempio, se nel trasmettere il dato di temperatura di una determinata città un determinato giorno si ometteva la seconda cifra decimale (15,2° C invece di 15,22° C), l’errore nell’elaborazione era considerato insignificante ai fini della riuscita della previsione. Valeva quindi l’assunto che, data una conoscenza approssimata dei valori iniziali, si sarebbe ottenuto un risultato sufficiente corretto nell’elaborazione del dato nel tempo, con un errore finale proporzionale all’errore d’immissione iniziale. Si trattava quindi, di una previsione di tipo deterministico, in cui, nell’ottica dei meteorologi del tempo, conoscendo lo stato presente del sistema in oggetto,  il suo futuro ed il suo passato diventano calcolabili con esattezza.

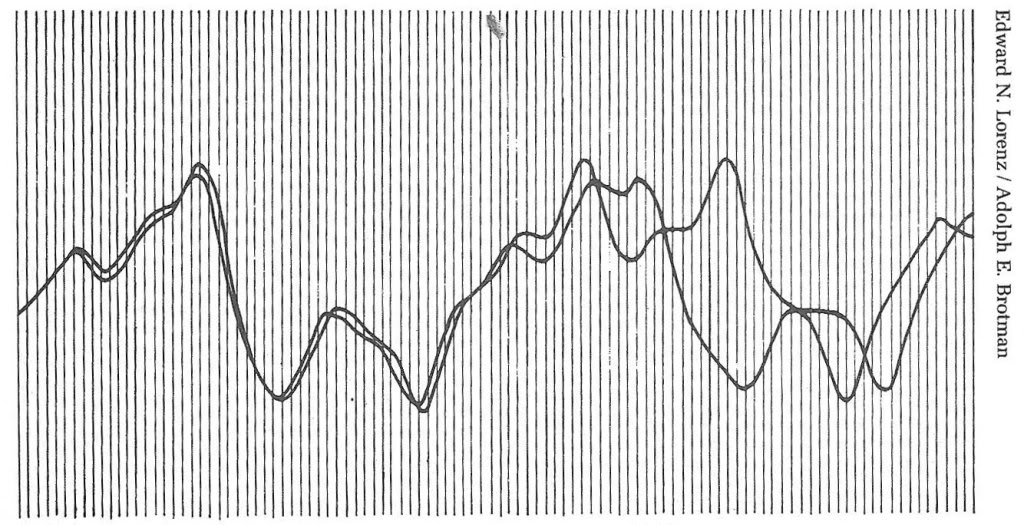
Ma le cose non stavano affatto così; come accennato all’inizio del racconto, un giorno nell’inverno del 1961, volendo esaminare una fase di elaborazione più lunga, nell’immettere nuovamente i dati e per far ripartire l’elaborazione stessa (andava fatto tutto a mano), Lorenz prese una scorciatoia. Anziché percorrere l’intero passaggio dal principio, calcolando l’evoluzione nel tempo dei vari parametri, cominciò a esaminarlo a metà del tracciato dell’elaborazione, inserendo gli stessi dati ma a una fase più avanzata del calcolo. Per dare al computer le condizione iniziali, introdusse i numeri prendendoli direttamente dallo stampato precedente e reinserendoli personalmente. Nell’inserire nuovamente i dati, per rapidità, ma anche perchè lo stampato forniva solo i valori fino alla terza cifra decimale, trascurò quindi tutti i decimali oltre la terza cifra (il computer prevedeva l’immissione fino alla sesta cifra decimale). Dopo circa un’ora, vide qualcosa di inatteso. L’elaborazione, perlomeno quella riguardante il medesimo periodo di tempo, avrebbe dovuto duplicare esattamente quella precedente. Lo stesso Lorenz aveva copiato i numeri da introdurre nel computer. Eppure, quando osservò lo stampato, vide i valori dei parametri divergere sempre più rapidamente dall’andamento della fase precedente, in maniera tale che, nel lungo periodo, ogni somiglianza con il tracciato precedente era sparita. La fig. 1 illustra uno dei tracciati originali analizzati da Lorentz in quella occasione, si vede come, al crescere del periodo di tempo considerato, aumenti la divergenza del dato iniziale, mentre come nel breve siano praticamente uguali.

Fig.1

Lo scienziato iniziò a confrontare quindi tutti i grafici ottenuti con le due modalità e si rese conto di un concetto fondamentale; ovvero, che la notevole divergenza nel lungo termine era causata da un apparentemente piccolo errore nell’immissione dei dati di input, lo scarto era quindi insito nella natura stessa del sistema. In sostanza, era impossibile fornire corrette previsioni meteorologiche nel lungo termine, in quanto anche il più piccolo errore nell’immissione del dato avrebbe generato una previsione completamente sballata nel lungo periodo. Era nato quindi lo studio della teoria del CAOS.

La portata dell’assunto stabilito da Lorentz era enorme, crollava tutto lo studio deterministico dei fenomeni fisici, nel senso che, perlomeno in campo meteorologico, non bastava conoscere il dato iniziale di un fenomeno per descriverlo nel tempo. Meglio ancora, i dati relativi alle condizioni iniziali avrebbero dovuto essere misurati con un’accuratezza teoricamente infinita per avere un’elaborazione corretta, e ciò é praticamente impossibile. Altrettanto impossibile è, quindi, effettuare una corretta previsione meteorologica nel lungo termine, mentre nel breve (ad esempio intorno le 96-120 h) la divergenza è sufficientemente piccola da consentire una buona accuratezza previsionale.

Qualche anno dopo, proprio in merito agli studi da lui effettuati, in un convegno a Città del Capo, Lorentz utilizzò il seguente esempio per descrivere il modello di comportamento caotico: “la perturbazione provocata dal battito delle ali di una farfalla a Città del Capo potrebbe provocare, dopo qualche giorno, radicali cambiamenti delle condizioni atmosferiche a Londra”. Era nata quindi, la definizione dell’effetto farfalla, il più classico degli esempi della teoria del caos.

Ma Lorentz andò anche oltre nei suoi studi; per simulare un comportamento caotico studiò il comportamento di alcuni sistemi cosiddetti “non lineari” dove, cioè, in presenza di più parametri, le variazioni di ciascuno di essi influenzavano in corso d’opera il valore degli altri. In particolare, per simulare un comportamento simile a quello che si ha durante la convezione atmosferica (i moti che generano i temporali ad esempio), utilizzò per gli esperimenti una ruota idraulica, ovvero una ruota, come quella di un mulino mostrata in figura 2, dove dall’alto veniva modificata gradualmente la quantità d’acqua che cadeva nel secchio. La tipologia di movimento di questa ruota al variare della quantità d’acqua immessa aveva un comportamento caotico, invertendo addirittura il senso di moto per un flusso troppo intenso ad esempio.

Fig.2

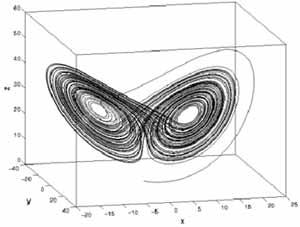
Lorentz individuò tre equazioni (non lineari), che potevano descrivere esattamente il moto di tale sistema idraulico e ne graficò i risultati. Ovvero graficò i valori delle tre variabili, inserite nelle tre equazioni, al variare della quantità d’acqua immessa dall’alto in caduta nel secchio e li graficò in un disegno a tre dimensioni, come quello riportato di seguito, nella figura 3 e 4.

Fig.3 

Fig.4

La figura riportata, nota come attrattore strano, riveste un’enorme importanza nello studio delle scienze meteorologiche e, più in generale della teoria del caos; con una similitudine poetica potremmo definirla l’immagine del caos. Questa strana figura infatti, rappresenta il modo di variare di tre grandezze, ad esempio temperatura, pressione e velocità del vento, in un sistema caotico. Ovvero, nonostante fosse apparentemente impossibile effettuare una previsione corretta della evoluzione nel tempo delle variabili citate, proprio per la difficoltà legata agli errori nella immissione nei dati, esisteva comunque una sorta di ordine nel caos, la variazione dei parametri aveva comunque una sorta di ripetitività, sebbene di inusitata complessità, che poteva essere rappresentata dall’attrattore strano sopra visualizzato…..

Le conseguenze degli studi di Lorentz furono, come intuibile, enormi nel campo della scienza; sulla teoria del caos si sarebbero basate tutte le simulazioni climatiche effettuate negli anni successivi. Tutti noi appassionati, ogni giorno,  “giochiamo” con i risultati degli studi ora esposti. Ad esempio, la più classica e fruibile applicazione della teoria del caos, nelle moderne elaborazioni disponibili in rete, sono le previsioni “ensemble” , di cui il prodotto più conosciuto sono i cosiddetti “spaghetti“.

Le ENS, come vengono comunemente definite e gli spaghetti, applicano alla lettera quanto sperimentato da Lorentz e, anzi, ripetono esattamente, più volte al giorno, l’esperimento, avvenuto in maniera fortuita nell’inverno del 1961.  In sostanza, nei dati di input, giunti dalle numerosissime stazioni meteorologiche diffuse in tutto il mondo, vengono  volutamente immessi degli errori, apparentemente insignificanti (qualche decimale) e viene quindi fatto girare il modello di calcolo. Grazie ai moderni calcolatori, tale operazione viene effettuata molte volte al giorno ed è possibile confrontare i dati ottenuti in tal modo con quelli invece ottenuti con i dati reali, non modificati. Se la divergenza è bassa anche nel medio e lungo termine, è probabile che la previsione sia abbastanza corretta anche a distanza di molti giorni.

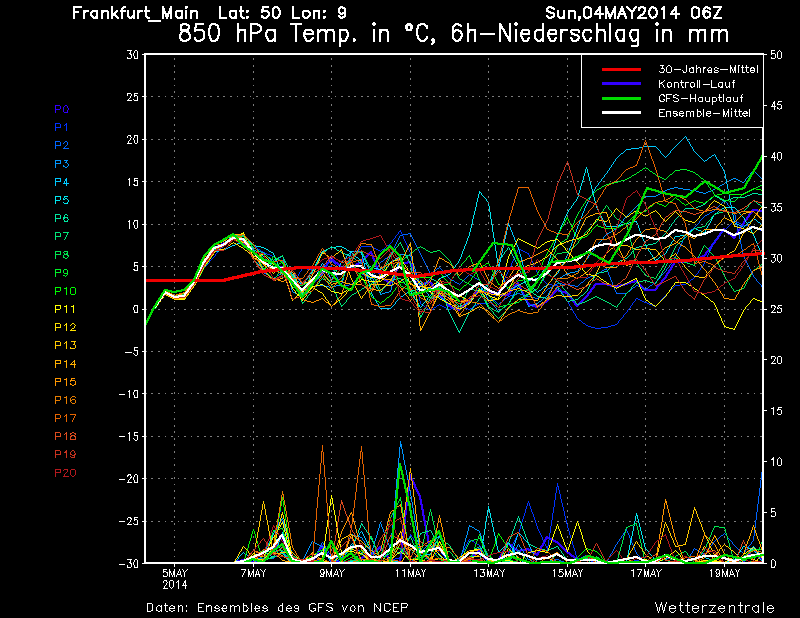
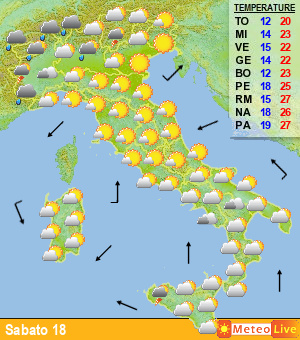
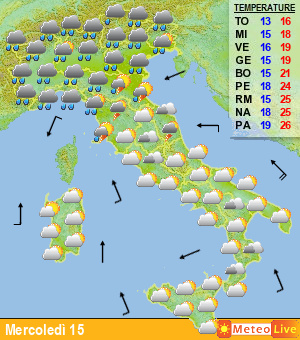
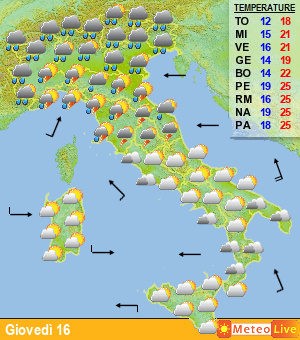
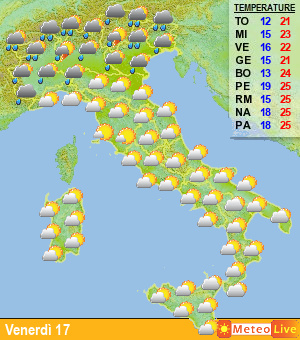
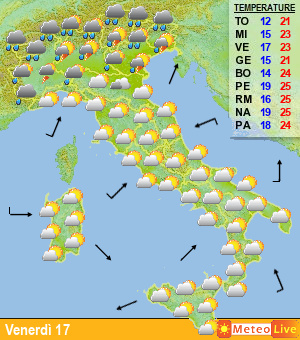
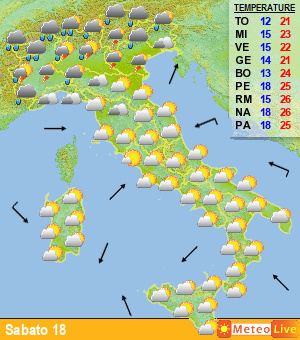
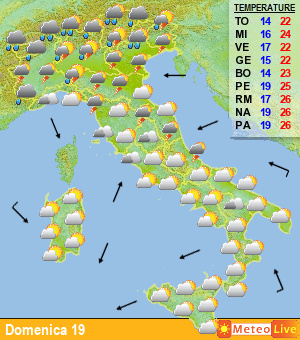
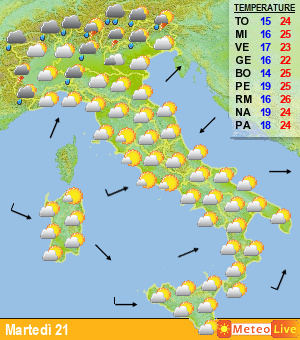
Passando agli esempi pratici, ecco una classica rappresentazione degli spaghetti; nella figura di seguito viene rappresentato un grafico in cui vengono riportati i valori di temperatura previsti a 850 hPa (1500 m) e le precipitazioni per la città di Francoforte, in Germania, nei prossimi 15 giorni (fig.5).

Fig.5

Ogni linea rappresenta una “perturbazione”, ovvero l’andamento del valore ottenuto modificando in maniera leggermente diversa i dati di input. Accanto a tali dati, con la linea in grassetto di colore verde, è presente anche l’elaborazione ottenuta con i dati reali, che può essere confrontata con gli altri valori.  Come si vede, man mano che aumenta il lasso temporale considerato (da sinistra verso destra), le linee divergono, proprio come accadeva con il grafico di Lorentz riportato in fig.1………

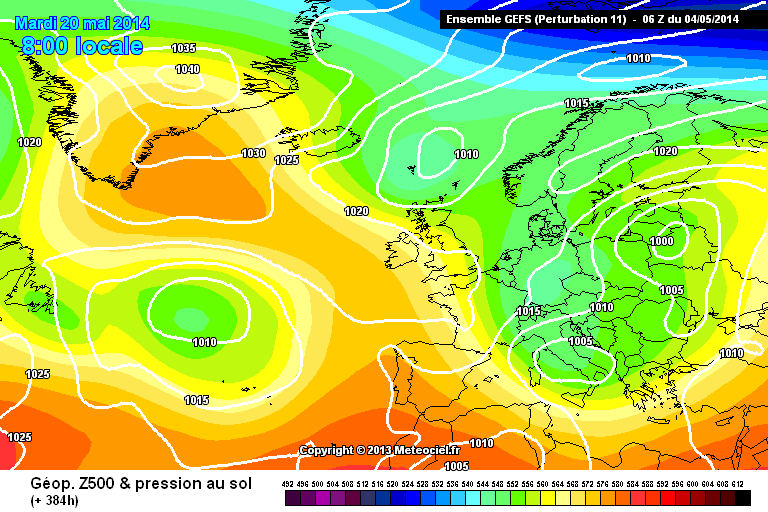
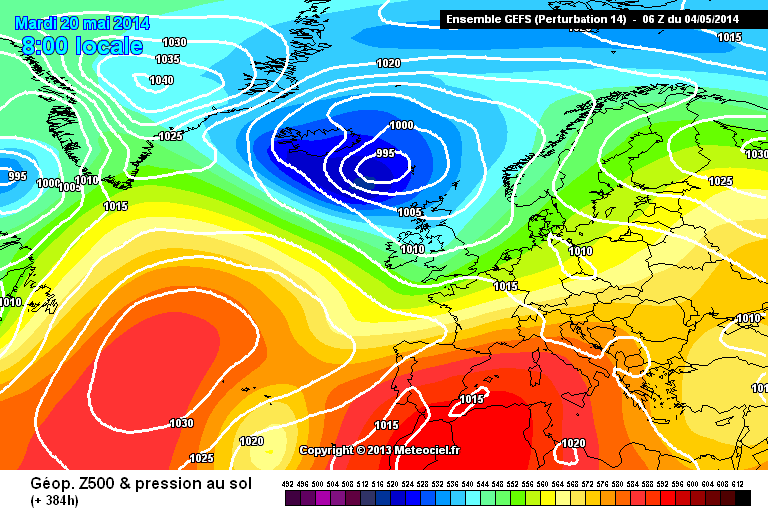
In rete è possibile vedere anche la restituzione grafica di ogni singola perturbazione e vengono fuori considerazioni molto interessanti. Ecco, ad esempio, riportata di seguito, la carta a 15 giorni dall’emissione dei valori di pressione a 500 hPa e al suolo di due delle “perturbazioni” riportate nel grafico in fig.5 (fig. 6 e 7)………

Fig. 6

Fig. 7

Come si vede dalle due figure , nella prima carta (fig.6) per il giorno 20 Maggio in Europa è prevista una saccatura fredda con maltempo in molte nazioni, fino a comprendere tutta la penisola italiana, mentre nella seconda immagine (fig.7) è visibile un’ampia rimonta dell’anticiclone delle Azzorre nel Mediterraneo, con caldo e bel tempo ormai affermati. Tutto ciò, con gli stessi dati di input modificati di un’inezia, ad esempio 1-2 centesimi di grado di temperatura e frazioni di hPa di pressione.

Quale migliore rappresentazione quindi della teoria del caos e della dipendenza sensibile dalle condizioni iniziali. Sarà quindi compito del tecnico preposto andare a valutare, in  maniera critica, la validità della previsione emessa, sulla base di questi tentativi, utili a capire in che direzione sta andando il tempo in una determinata area.

Ovviamente, nel breve le cose sono più semplici, sebbene ne ora ne mai sarà possibile definire esattamente il tempo di una giornata in un determinato luogo, in quanto l’errore è insito nell’impostazione del modello e nella caoticità del sistema. Come abbiamo accennato in precedenza, è praticamente impossibile inserire infatti dati di una precisione infinita ne modello di calcolo e, pertanto, è impossibile conoscere esattamente il tempo di una determinata regione, anche nel breve, sebbene attualmente se ne possa avere una buona approssimazione. Per quanto riguarda il lungo termine, ancora per moltissimi anni la previsione oltre i 15 giorni, ma anche prima, rappresenterà semplicemente una tendenza approssimata della realtà. Occorre pertanto diffidare di chi propone con troppa facilità e/o con troppa precisione le tendenza stagionali future o, addirittura, quelle nei prossimi anni…

Nelle linee generali comunque, alcuni criteri possono essere stabiliti; lo studio delle tendenze stagionali è una scienza in continuo approfondimento e stabilire, ad esempio, se l’estate futura sarà particolarmente calda, in alcuni casi, potrebbe essere possibile, ma solo, ripetiamo, nelle linee generali.

Per concludere, la cosa più bella da affermare è che non ci sarà mai una giornata uguale a un’altra dal punto di vista meteorologico in nessun luogo del mondo e questo aspetto rappresenta sicuramente la cosa più bella nello studio della meteorologia.

Ciao ciao

Ilario Larosa (meteogeo)